お詫びと訂正 インターフェース誌 2015年 4月号 p56

過去に執筆した記事に誤りがありましたため下記の通り訂正致します．謹んでお詫び申し上げます．

2015年4月号 p56 ノッチフィルタの伝達関数の訂正

-3 dB バンド幅 ω_b にプリワーピングを適用していなかったため，Q値が実際よりも高い値に相当する特性となっておりました．正規化された中心周波数が高い場合，特に影響があります．

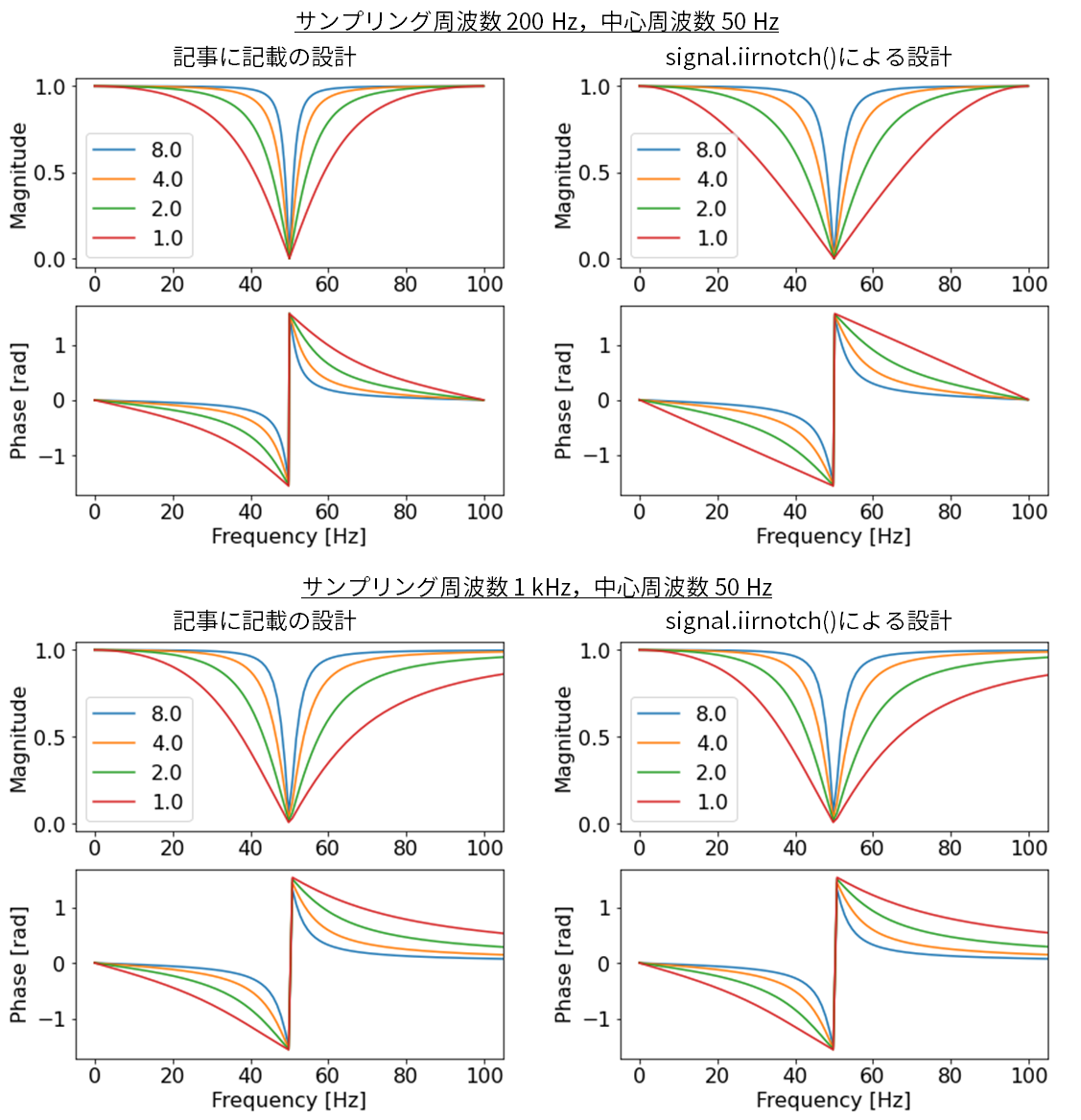
具体的には，下図の通りサンプリング周波数 200 SPSで，中心周波数 50 Hzのノッチフィルタを掛けた場合，記事の設計では，Python の SciPy ライブラリ signal.iirnotch() 関数で設計した場合に比べてシャープな特性となってしまっています．

サンプリング周波数 1 kSPSの場合は，パッと見た目には分からない程度の差異しかありません．
当時の記事では，サンプリング周波数 1 kSPS，遮断周波数 50 または 60 Hzで使用しており，その範囲においては実用上問題ありません．

signal.iirnotch() と同様の結果となる伝達関数は以下の通りです．（バンド幅 -3dB固定の場合）

余談ながら，signal.iirnotch() が追加されたのは，SciPy 0.19.0 (SciPy v1.5.4)で，2017/3/9とのことです．MATLABでは，iirnotch()は，R2011a追加とあるので2011年です．MATLABでは検証できる環境にあったようです．

2次IIRノッチフィルタ伝達関数の導出過程：

アナログノッチフィルタの伝達関数は，
$$G\left(s\right)=\frac{s^2+\omega_0^2}{s^2+\frac{\omega_0}{Q}s+\omega_0^2}$$
で与えられます．Q値の定義式，
$$Q=\frac{\omega_0}{\omega_b}$$
を代入して，下式のようにも書けます．
$$G\left(s\right)=\frac{s^2+\omega_0^2}{s^2+\omega_bs+\omega_0^2}$$

中心周波数 ω₀ をプリワーピングにより補正します．
$$\omega_0\rightarrow\omega_{0A}=\frac{2}{T}\ \tan{\left(\frac{\omega_0T}{2}\right)}$$

-3dB バンド幅 ω_b に対してもプリワーピングを適用します．（ここが訂正箇所です）
$$\omega_b=\omega_{c2}-\omega_{c1}$$
$$\rightarrow\omega_{bA}=\frac{2}{T}\left(\tan{\left(\frac{\omega_{c2}T}{2}\right)}-\tan{\left(\frac{\omega_{c1}T}{2}\right)}\right)$$
ここで，
$$\frac{2}{T}\tan{\left(\frac{\omega_bT}{2}\right)}=\frac{2}{T}\tan{\left(\frac{\left(\omega_{c2}-\omega_{c1}\right)T}{2}\right)}$$
$$=\frac{2}{T}\frac{\tan{\left(\frac{\omega_{c2}T}{2}\right)}-\tan{\left(\frac{\omega_{c2}T}{2}\right)}}{1+\tan{\left(\frac{\omega_{c2}T}{2}\right)}\tan{\left(\frac{\omega_{c1}T}{2}\right)}}$$
$$=\frac{\omega_{bA}}{1+\tan{\left(\frac{\omega_{c2}T}{2}\right)}\tan{\left(\frac{\omega_{c1}T}{2}\right)}}$$
$$\Leftrightarrow\omega_{bA}=\left(1+\tan{\left(\frac{\omega_{c2}T}{2}\right)}\tan{\left(\frac{\omega_{c1}T}{2}\right)}\right)\frac{2}{T}\tan{\left(\frac{\omega_bT}{2}\right)}$$
であり，
$$\omega_{c2A}\omega_{c1A}=\omega_{0A}^2$$
$$\Leftrightarrow\tan{\left(\frac{\omega_{c2}T}{2}\right)}\tan{\left(\frac{\omega_{c1}T}{2}\right)}=\tan^2{\left(\frac{\omega_0T}{2}\right)}$$
より，プリワーピング後のバンド幅は，
$$\omega_{bA}=\frac{2}{T}\left(1+{\tan}^2{\left(\frac{\omega_0T}{2}\right)}\right)\tan{\left(\frac{\omega_bT}{2}\right)}$$
と書くことができます．

プリワーピングにより周波数を補正した伝達関数，
$$G\left(s\right)=\frac{s^2+\omega_{0A}^2}{s^2+\omega_{bA}s+\omega_{0A}^2}$$
に，双一次変換，
$$s=\ \frac{2}{T}\ \frac{1-z^{-1}}{1+z^{-1}}$$
を適用すると，全ての項に2/Tの2乗が含まれているので省略し，また簡略化のために，
$$\omega_{0A}=\frac{2}{T}\tan{\left(\frac{\omega_0T}{2}\right)}\equiv\frac{2}{T}\Omega$$
$$\omega_{bA}=\frac{2}{T}\left(1+\Omega^2\right)\tan{\left(\frac{\omega_bT}{2}\right)}\equiv\frac{2}{T}\alpha$$
と定義すると，伝達関数は，
$$G\left(s\right)=\frac{\left(\ \frac{1-z^{-1}}{1+z^{-1}}\right)^2+\Omega^2}{\left(\frac{1-z^{-1}}{1+z^{-1}}\right)^2+\alpha\left(\frac{1-z^{-1}}{1+z^{-1}}\right)+\Omega^2}$$
$$=\ \frac{\left(1-z^{-1}\right)^2+\Omega^2\left(1+z^{-1}\right)^2}{\left(1-z^{-1}\right)^2+\left(1+\Omega^2\right)\alpha\left(1-z^{-2}\right)+\Omega^2\left(1+z^{-1}\right)^2}$$
$$=\ \frac{\left(1+\Omega^2\right)-2{\left(1-\Omega^2\right)z}^{-1}+\left(1+\Omega^2\right)z^{-2}}{\left(1+\Omega^2+\alpha\right)-2{\left(1-\Omega^2\right)z}^{-1}+\left(1-\alpha+\Omega^2-\alpha\right)z^{-2}}$$
$$=\left(\frac{1+\Omega^2}{1+\Omega^2+\alpha}\right)\ \frac{1-2{\frac{1-\Omega^2}{1+\Omega^2}z^{-1}}+z^{-2}}{1-2{\frac{1-\Omega^2}{1+\Omega^2+\alpha}z^{-1}}+\frac{1+\Omega^2-\alpha}{1+\Omega^2+\alpha}z^{-2}}$$
と変形されます．
ここで，
$$\alpha=\left(1+\Omega^2\right)\beta$$
とおくと，各項の係数は，
$$\frac{1+\Omega^2}{1+\Omega^2+\alpha}=\frac{1}{1+\beta}$$
$$\frac{1-\Omega^2}{1+\Omega^2}=\frac{1-\tan^2{\left(\frac{\omega_0T}{2}\right)}}{1+\tan^2{\left(\frac{\omega_0T}{2}\right)}}=\cos{\left(\omega_0T\right)}$$
$$\frac{1-\Omega^2}{1+\Omega^2+\alpha}=\frac{1-\Omega^2}{1+\Omega^2}\frac{1}{1+\beta}=\frac{\cos{\left(\omega_0T\right)}}{1+\beta}$$
$$\frac{1+\Omega^2-\alpha}{1+\Omega^2+\alpha}=\frac{1-\beta}{1+\beta}$$
となるので，伝達関数は下式となります．
$$G\left(s\right)=\frac{1}{1+\beta}\ \frac{1-2{\cos{\left(\omega_0T\right)}z}^{-1}+z^{-2}}{1-2{\frac{\cos{\left(\omega_0T\right)}}{1+\beta}z}^{-1}+\frac{1-\beta}{1+\beta}z^{-2}}$$
ここで，
$$b=\frac{1}{1+\beta}$$
とおくと，最終的な2次IIRノッチフィルタの伝達関数，
$$H\left(z\right)=b\ \frac{1-2{\cos{\left(\omega_0T\right)}z}^{-1}+z^{-2}}{1-2b{\cos{\left(\omega_0T\right)}z}^{-1}+\left(2b-1\right)z^{-2}}$$
が得られます．
ただし，
$$b=\frac{1}{1+\beta}=\frac{1}{1+\frac{\alpha}{1+\Omega^2}}$$
となり，ω_bA を 2/T×αと置いた式より，
$$\left(1+\Omega^2\right)\tan{\left(\frac{\omega_bT}{2}\right)}=\alpha$$
を代入すると，bは，
$$b=\frac{1}{1+\tan{\left(\frac{\omega_bT}{2}\right)}}$$
または，
$$b=\frac{1}{1+\tan(\frac{\omega_0T}{2Q})}$$
となります．

【参考】
Sophocles J. Orfanidis, “Introduction To Signal Processing”, Prentice-Hall, 1996